东喜玛拉雅研究院实创部学术论坛

地点：S3-330

时间：2017年6月4日  14:00－15:00

参与人员：大理大学东喜玛拉雅研究院实创部全体成员、黄志旁老师

验证生日悖论

汇报人：顾斐（空间分析组）

　　汇报人首先简单地介绍了何为生日悖论，其次介绍了验证基本思路：通过r statistic 软件取已有数据（数据来源：大理大学农学与生物科学学院14、15、16级各专业学生（644个）），随机抽取数据，每次抽取一定数目（23、50），重复循环10000次，统计并计算出概率值；介绍了大致的程序内容并展示了实验结果：

　　1、随机抽取23人：6687次抽取中有人重复生日（即出现概率为66.87%）

　　2、随机抽取50人：9956次抽取中有人重复生日（即出现概率为99.56%）

　　实验结果验证了生日悖论，且实际数据比理论数据更大，其原因可能与地方升学政策、自然生理情况有关。

　　此外，还讲述了两个拓展的探索实验：随机抽样人数是否对重复概率产生影响？抽样强度对重复概率是否产生影响？通过替换程序中的参数得出结果为：随着抽样人数的上升，重复生日的概率也逐步上升；抽样强度的确会对结果造成影响，抽样强度越大，结果的标准差值更小。

　　图/张小玉   文/顾斐

　　此外，顾荣（空间分析组）就其他议题也做了汇报。

附：生日悖论小论文　　

　　验证生日悖论

　　空间分析小组科协项目

　　悖论：称为吊诡或诡局，是指一种导致矛盾的命题。通常从逻辑上无法判断正确或错误称为悖论，似非而是称为佯谬；有时候违背直觉的正确论断也称为悖论。

　　一、问题引入：

　　生日悖论：如果在一个房间有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%；50人中两人生日相同的概率甚至达到了97%（严加安.2012.中国学报）。这就意味着在一个典型的标准小学班级(30人)中，存在两人生日相同的可能性更高。大多数人会认为，23人中有2人生日相同的概率应该远远小于50%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论，从这个数学事实与一般直觉相抵触的意义上，它才称得上是一个悖论。

　　二、数据来源：

　　为保证生日数据的准确性，经学办老师同意获得，我们获得农生院14、15、16级各专业的同学的生日数据共644个。

　　三、分析：

　　方法：利用R软件对数据进行统计分析。

　　步骤：将收集得到的生日数据取月日部分，统计为四位数的格式（1225即12月25日）→ 利用R语言分析（导入csv格式中的数据到R，编程，通过循环10000次分别随机抽取23人、50人进行实验统计，最后计算出百分比）

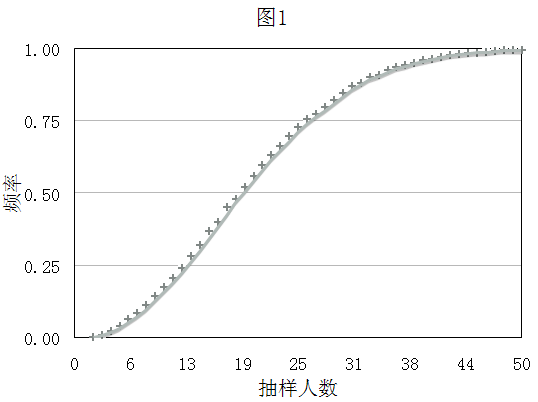
　　结论：在644个数据中，我们首先随机抽取23人进行比对，循环10000次的结果为：有6687次抽取的随机23人重复生日（即出现概率为66.87%）。其次，随机抽取50人进行比对，循环10000次的结果为：有9956次抽取的随机50人重复生日（即出现概率为99.56%）（图1）。我们的实验结果验证了文献中提出的生日悖论问题，而且实际得出结果比理论更大。从实际来考虑，比理论还高的结果除了本身的高概率之外，可能与地方区域升学政策、自然生理情况也有很大关系。

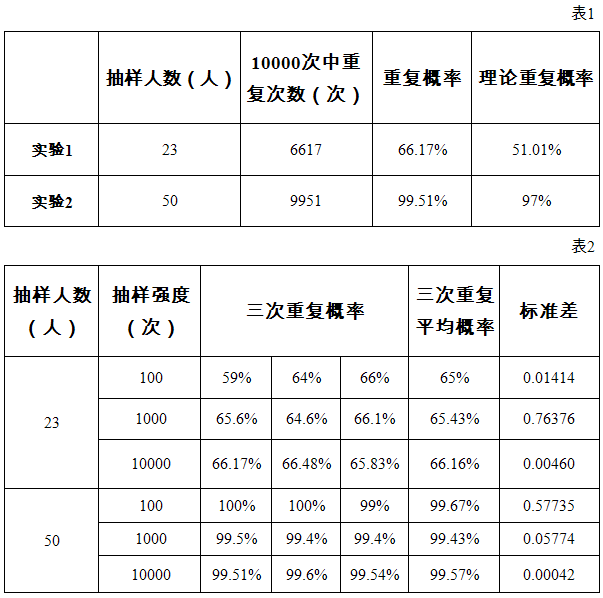
　　在验证了结论后，我们再对抽样人数对重复概率的影响及抽样强度对结果的影响进行试验分析。(结果见图1、表2。)

　　由图1可知，重复概率随抽样人数的增加而逐步增加，当抽样人数到达37人左右时，概率的改变基本趋于平缓。

　　由表2可知，抽样强度对于重复概率会有影响、不同抽样人数下的抽样强度对重复概率也会有影响。总体来说抽样强度越大，结果所得出的重复概率越稳定。因此，实验中应加大抽样强度（即可以循环抽取10000次）。相对的，实验中抽样人数增多也应该相应提高抽样强度以保证结果。